Nieuwland et al replication attempts of DeLong at al. 2005
Shravan Vasishth
4/1/2017
Note: Revised 8 April 2017 following comments from Nieuwland and others.
Recently, Nieuwland et al did an interesting series of replication attempts of the DeLong et al 2005 Nature Neuroscience paper. Nieuwland et al report a failure to replicate the original effect. This is just a quick note to suggest that it may be difficult to claim that this is a replication failure. I focus only on the article data.
First we load the Nieuwland et al data (available from https://osf.io/eyzaq).
articles <-read.delim("public_article_data.txt", quote="")
#head(articles)Then make sure columns are correct data types, and get lab names, convert cloze to z-scores as Nieuwland et al did:
articles$item <-as.factor(articles$item)
articles$cloze <- as.numeric(as.character(articles$cloze))
labnames<-unique(articles$lab)
# Z-transform cloze and prestimulus interval
articles$zcloze <- scale(articles$cloze, center = TRUE, scale = TRUE)
articles$zprestim <- scale(articles$prestim, center = TRUE, scale = TRUE)Then use lmer to compute estimates from each lab separately. I also fit ``maximal’’ models in Stan (HT: Barr et al 2013 ;) but nothing much changes so I use these varying slopes models without correlations:
library(lme4)## Loading required package: Matrix# models for article fit for each lab separately:
res<-matrix(rep(NA,9*2),ncol=2)
for(i in 1:9){
model <- lmer(base100 ~ zcloze + ( 1| subject) +
(zcloze|| item),
data = subset(articles,lab==labnames[i]),
control=lmerControl(
optCtrl=list(maxfun=1e5)))
res[i,]<-summary(model)$coefficients[2,1:2]
}Next, we fit a random-effects meta-analysis using the nine-labs replications.
Random effects meta-analysis:
The model specification was as follows.
Assume that:
- \(y_i\) is the observed effect in microvolts in the \(i\)-th study with \(i=1\dots n\);
- \(\theta\) is the true (unknown) effect, to be estimated by the model;
- \(\sigma_{i}^2\) is the true variance of the sampling distribution; each \(\sigma_i\) is estimated from the standard error available from the study \(i\);
- The variance parameter \(\tau^2\) represents between-study variance.
We can construct a random-effects meta-analysis model as follows:
\[\begin{equation} \begin{split} y_i \mid \theta_i,\sigma_i^2 \sim & N(\theta_i, \sigma_i^2) \quad i=1,\dots, n\\ \theta_i\mid \theta,\tau^2 \sim & N(\theta, \tau^2), \\ \theta \sim & N(0,10^2),\\ \tau \sim & N(0,10^2)T(0,) \hbox{(truncated normal)} \\ \end{split} \end{equation}\]The priors shown above are just examples. Other priors can be used and are probably more suitable in this case. I use Gelman et al 2014’s non-centralized parameterization in any case in the Stan code below because of the sparse data we have here.
## Stan meta-analysis:
library(rstan)## Loading required package: ggplot2## Loading required package: StanHeaders## rstan (Version 2.14.1, packaged: 2017-01-20 19:24:23 UTC, GitRev: 565115df4625)## For execution on a local, multicore CPU with excess RAM we recommend calling
## rstan_options(auto_write = TRUE)
## options(mc.cores = parallel::detectCores())rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
dat<-list(y=res[,1],n=length(res[,1]),s=res[,2])
## is this the DeLong et al mean and se? Could add it to meta-analysis if original data ever becomes available.
#dat$y<-c(dat$y,0.4507929)
#dat$s<-c(dat$s,.5)
#dat$n<-dat$n+1
fit <- stan(file='rema2.stan', data=dat,
iter=2000, chains=4, seed=987654321,
control = list(adapt_delta = 0.99))
paramnames<-c("mu","tau","theta")
print(fit,pars=paramnames,prob=c(0.025,0.975))## Inference for Stan model: rema2.
## 4 chains, each with iter=2000; warmup=1000; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
##
## mean se_mean sd 2.5% 97.5% n_eff Rhat
## mu 0.11 0 0.07 -0.04 0.25 2153 1
## tau 0.11 0 0.08 0.00 0.31 1496 1
## theta[1] 0.11 0 0.10 -0.09 0.31 4000 1
## theta[2] 0.13 0 0.10 -0.08 0.36 4000 1
## theta[3] 0.10 0 0.11 -0.13 0.33 4000 1
## theta[4] 0.10 0 0.11 -0.13 0.30 4000 1
## theta[5] 0.03 0 0.11 -0.23 0.22 4000 1
## theta[6] 0.06 0 0.13 -0.25 0.27 4000 1
## theta[7] 0.14 0 0.11 -0.05 0.39 4000 1
## theta[8] 0.18 0 0.11 0.00 0.42 4000 1
## theta[9] 0.15 0 0.11 -0.04 0.40 4000 1
##
## Samples were drawn using NUTS(diag_e) at Sat Apr 8 19:51:28 2017.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at
## convergence, Rhat=1).params<-extract(fit,pars=paramnames)Results
The interesting thing here is the posterior distribution of \(\mu\), the effect of cloze probability on the N400.
## posterior probability that mu is > 0:
mean(params$mu>0)## [1] 0.9345mean(params$mu)## [1] 0.1084961## lower and upper bounds of credible intervals:
lower<-quantile(params$mu,prob=0.025)
upper<-quantile(params$mu,prob=0.975)
SE<-(upper-lower)/4 ## approximate, assuming symmetry which seems reasonable here
hist(params$mu,main="Posterior distribution of effect \n Article",xlab="mu",freq=F)
abline(v=0)
arrows(x0=lower,y0=1,x1=upper,y1=1,angle=90,code=3)Thus, even in the Nieuwland et al nine-labs data, the N400 amplitude decreases (becomes more positive) with increasing cloze probability. The posterior probability that the coefficient for cloze is greater than 0 is 94%. From this, one cannot really say that the Nieuwland et al studies are a failure to replicate the DeLong study.
The next step would be to compare the original DeLong et al data using the same analysis done above. But I was unable to get the original data up until now, so I’m posting my comment on my blog.
Prestimulus interval
Mante Nieuwland pointed out to me that the effect can be seen already in the prestimulus interval. Here is the evidence for that.
# models for article fit for each lab separately:
res<-matrix(rep(NA,9*2),ncol=2)
for(i in 1:9){
model <- lmer(prestim ~ zcloze + ( 1| subject) +
(zcloze|| item),
data = subset(articles,lab==labnames[i]),
control=lmerControl(
optCtrl=list(maxfun=1e5)))
res[i,]<-summary(model)$coefficients[2,1:2]
}
dat<-list(y=res[,1],n=length(res[,1]),s=res[,2])
## is this the DeLong et al mean and se? Could add it to meta-analysis if original data ever becomes available.
#dat$y<-c(dat$y,0.4507929)
#dat$s<-c(dat$s,.5)
#dat$n<-dat$n+1
fit <- stan(file='rema2.stan', data=dat,
iter=2000, chains=4, seed=987654321,
control = list(adapt_delta = 0.99))
paramnames<-c("mu","tau","theta")
print(fit,pars=paramnames,prob=c(0.025,0.975))## Inference for Stan model: rema2.
## 4 chains, each with iter=2000; warmup=1000; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
##
## mean se_mean sd 2.5% 97.5% n_eff Rhat
## mu 0.07 0 0.07 -0.06 0.21 1497 1
## tau 0.12 0 0.08 0.01 0.30 897 1
## theta[1] 0.18 0 0.11 0.00 0.41 2632 1
## theta[2] -0.01 0 0.11 -0.26 0.17 2042 1
## theta[3] 0.11 0 0.11 -0.10 0.36 4000 1
## theta[4] 0.13 0 0.10 -0.04 0.34 4000 1
## theta[5] 0.03 0 0.09 -0.16 0.20 4000 1
## theta[6] 0.01 0 0.11 -0.23 0.20 4000 1
## theta[7] 0.03 0 0.10 -0.19 0.22 4000 1
## theta[8] 0.09 0 0.09 -0.08 0.28 4000 1
## theta[9] 0.11 0 0.09 -0.06 0.29 4000 1
##
## Samples were drawn using NUTS(diag_e) at Sat Apr 8 19:51:33 2017.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at
## convergence, Rhat=1).params<-extract(fit,pars=paramnames)
## posterior probability that mu is > 0:
mean(params$mu>0)## [1] 0.88175mean(params$mu)## [1] 0.07359659## lower and upper bounds of credible intervals:
lower<-quantile(params$mu,prob=0.025)
upper<-quantile(params$mu,prob=0.975)
SE<-(upper-lower)/4 ## approximate, assuming symmetry which seems reasonable here
hist(params$mu,main="Posterior distribution of effect \n Prestimulus interval",xlab="mu",freq=F)
abline(v=0)
arrows(x0=lower,y0=1,x1=upper,y1=1,angle=90,code=3)Retrospective power calculation
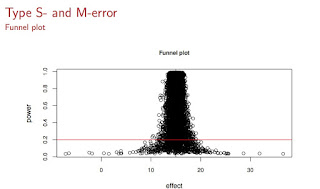
We now compute retrospective power and Type S/M errors:
## Gelman and Carlin function:
retrodesign <- function(A, s, alpha=.05, df=Inf, n.sims=10000){
z <- qt(1-alpha/2, df)
p.hi <- 1 - pt(z-A/s, df)
p.lo <- pt(-z-A/s, df)
power <- p.hi + p.lo
typeS <- p.lo/power
estimate <- A + s*rt(n.sims,df)
significant <- abs(estimate) > s*z
exaggeration <- mean(abs(estimate)[significant])/A
return(list(power=power, typeS=typeS, exaggeration=exaggeration))
}
retrodesign(.11, SE)## $power
## 97.5%
## 0.3761173
##
## $typeS
## 97.5%
## 0.0004168559
##
## $exaggeration
## [1] 1.616742The bad news here is that if the meta-analysis posterior mean for the article is the true effect, then power is about 34%.
If we want about 80% power, we need to halve that SE:
retrodesign(.11, 0.072/2)## $power
## [1] 0.8633715
##
## $typeS
## [1] 3.063012e-07
##
## $exaggeration
## [1] 1.079705I think that implies that you need four times as many subjects than you had.
Acknowledgements
Thanks to Mante Nieuwland and Stephen Politzer-Ahles for patiently explaining a lot of details to me, and for sharing their data and code.
Appendix: Stan code
Here is the meta-analysis Stan code with the Gelman-style reparameterization. y_tilde is not used above, but yields posterior predictive values, and could be used profitably in future replication attempts.
data {
int<lower=0> n; //number of studies
real y[n]; // estimated effect
real<lower=0> s[n]; // SEs of effect
}
parameters{
real mu; //population mean
real<lower=0> tau; // between study variability
vector[n] eta; //study level errors
}
transformed parameters {
vector[n] theta; // study effects
theta = mu + tau*eta;
}
model {
eta ~ normal(0,1);
y ~ normal(theta,s);
}
generated quantities{
vector[n] y_tilde;
for(i in 1:n){
y_tilde[i] = normal_rng(theta[i],s[i]);
}
}