Should we fit maximal linear mixed models?

Recently, Barr et al published a paper in the Journal of Memory and Language, arguing that we should fit maximal linear mixed models, i.e., fit models that have a full variance-covariance matrix specification for subject and for items. I suggest here that the recommendation should not be to fit maximal models, the recommendation should be to run high power studies.

I released a simulation on this blog some time ago arguing that the correlation parameters are pretty meaningless.  Dale Barr and Jake Westfall replied to my post, raising some interesting points. I have to agree with Dale's point that we should reflect the design of the experiment in the analysis; after all, our goal is to specify how we think the data were generated. But my main point is that given the fact that the culture in psycholinguistics is to run low power studies (we routinely publish null results with low power studies and present them as positive findings), fitting maximal models without asking oneself whether the various parameters are reasonably estimable will lead us to miss effects.

For me, the only useful recommendation to psycholinguists should be to run high power studies.

Consider two cases:

1. Run a low power study (the norm in psycholinguistics) where the null hypothesis is false.

If you blindly fit a maximal model, you are going to miss detecting the effect more often compared to when you fit a minimal model (varying intercepts only). For my specific example below, the proportions of false negatives is 38% (maximal) vs 9% (minimal).

In the top figure, we see that under repeated sampling, lmer is failing to estimate the true correlations for items (it's doing a better job for subjects because there is more data for subjects). Even though these are nuisance parameters, trying to estimate them for items in this dataset is a meaningless exercise (and the fact that the parameterization is going to influence the correlations is not the key issue here---that decision is made based on the hypotheses to be tested).

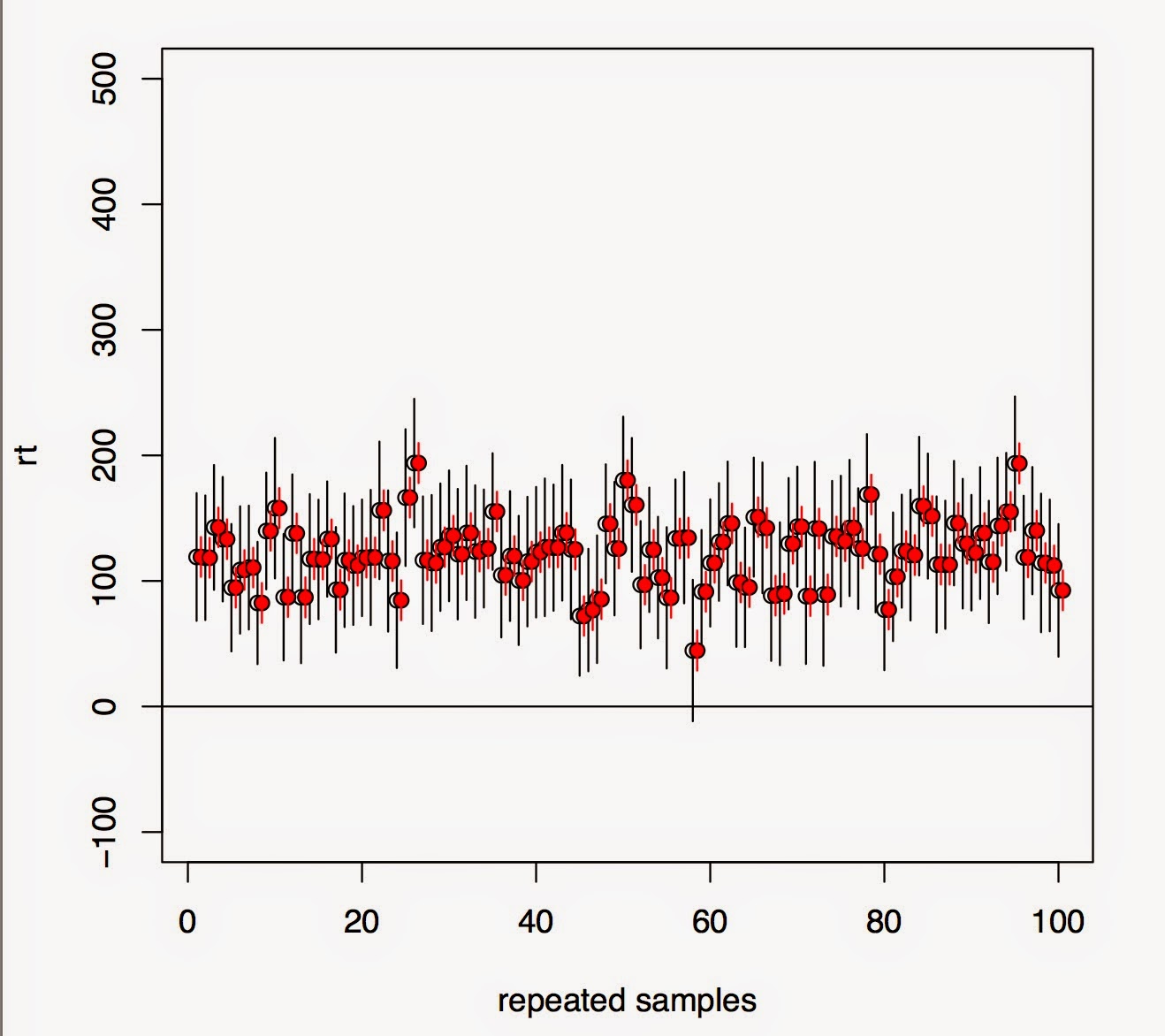
The lower figure shows that under repeated sampling, the effect (\mu is positive here, see my earlier post for details) is being missed much more often with a maximal model (black lines, 95% CIs) than with a varying intercepts model (red lines). The difference is in the miss probability is 38% (maximal) vs 9% (minimal).



2. Run a high power study.

Now, it doesn't really matter whether you fit a maximal model or not. You're going to detect the effect either way. The upper plot shows that under repeated sampling, lmer will tend to detect the true correlations correctly. The lower plot shows that in almost 100% of the cases, the effect is detected regardless of whether we fit a maximal model (black lines) or not (red lines).

My conclusion is that if we want to send a message regarding best practice to psycholinguistics, it should not be to fit maximal models. It should be to run high power studies. To borrow a phrase from Andrew Gelman's blog (or from Rob Weiss's), if you are running low power studies, you are leaving money on the table.

Here's my code to back up what I'm saying here. I'm happy to be corrected!

https://gist.github.com/vasishth/42e3254c9a97cbacd490