I wanted to post this reply to John Kruschke's blog post, but the blog comment box does not allow such a long response, so I posted it on my own blog and will link it in the comment box:
Hi John,
thanks for the detailed responses, and for the friendly tone of your response, I appreciate it.
I will try to write a more detailed review of the book to give some suggestions for the next edition, but I just wanted to respond to your comments:
1. Price: I agree that it's relative. But your argument assumes a US audience; people are often willing to pay outrageous amounts for things that are priced much more reasonably (and realistically) in Europe. Is the book primarily targeted to the US population? If not, the price is unreasonable. I cannot ask my students to buy this book when much cheaper ones exist. Even Gelman et al release slides that cover the entire or a substantial part of the BDA book. The analogy with calculus book is not valid either; Gilbert Strang's calculus book is available free on the internet, and there are many other free textbooks of very high quality. For statistics, there's Kerns, Michael Lavine's book, and for probability there are several great books available for free.
This book is more accessible than BDA and could become the standard text in psycholinguistics/psychology/linguistics. Why not halve the price and make it easier to get hold of? Even better, release a free version on the web. I could then even set it as a textbook in my courses, and I would.
2. Regarding the frequentist discussion, you wrote: "The vast majority of users of traditional frequentist statistics don't know why they should bother with taking the effort to learn Bayesian methods."
and
"Again, I think it's important for beginners to see the contrast with frequentist methods, so that they know why to bother with Bayesian methods."
My objection is that the criticism of frequentist methods is not the primary motivation for using Bayesian methods. I agree that people don't understand p-values and CIs. But the solution to that is to educate them so they understand them, the motivation for using Bayes cannot be that people don't understand frequentist methods
and/or abuse them. The next step would be to not use Bayesian methods because people who use it don't understand them and/or abuse them.
The primary motivation for me for using Bayes is the astonishing flexibility of Bayesian tools. It's not the only motivation, but this one thing outweighs everything else for me.
Also, even if the user of frequentist statistics realizes the problems inherent in the abuse of frequentist tools, this alone won't be sufficient to motivate them to move to Bayesian statistics. A more inclusive philosophy would be more effective: for some things a frequentist method is just fine (used properly). For other things you really need Bayes. You don't always need a laser gun; there are times when a hammer would do just fine (my last sentence does not do justice to frequentist tools, which are often really sophisticated).
3. "If anything, I find that adherence to frequentist methods require more blind faith than Bayesian methods, which to me just make rational sense. To the extent there is any tone of zealotry in my writing, it's only because the criticisms of p values and confidence intervals can come as a bit of a revelation after years of using p values without really understanding them."
I understand where you are coming from; I have also taken the same path of slowly coming to understand what the methodology was really saying, and initially I also fell into the trap of getting annoyed with frequentist methods and rejecting them outright.
But I have reconsidered my position and I think Bayes should be presented on its own merits. I can see that relating Bayes and freq. methods is necessary to clarify the differences, but this shouldn't run out of control. In my future courses that is the line I am going to take.
When I read material attacking frequentist methods *as a way to get to Bayes*, I am strongly reminded of the gurus in India who use a similar strategy to make their new converts believe in them and drive out any loyalty to the old guru. That is where my analogy to religion is coming from. It's an old method, and I have seen religious zealots espousing "the one right way" using it.
4. "Well, yes, that is a major problem. But I don't think it's the only major problem. I think most users of frequentist methods don't understand what a p value and confidence interval really are. "
Often, these are the same thing. They are abused by many people because they don't understand them. An example is psycholinguistics, where we routinely publish null results in low power experiments as positive findings. The people who do that are not abusing statistics deliberately, they just don't know that a null result is not informative in their particular settings. Journal editors (top journals) think that a lower p-value gives you more evidence in favor of the specific alternative. They just don't understand it, but they are not involved in deception.
The set of people who understand the method and deliberately abuse it is probably nearly the empty set. I don't know anyone in psycholinguistics who understands p-values and CIs and still abuses the method.
I'll write more later (and I have many positive comments!) once I've finished reading your 700+ page book! :)
This blog is a repository of cool things relating to statistical computing, simulation and stochastic modeling.
Search
Sunday, November 30, 2014
Tuesday, November 25, 2014
Should we fit maximal linear mixed models?
Recently, Barr et al published a paper in the Journal of Memory and Language, arguing that we should fit maximal linear mixed models, i.e., fit models that have a full variance-covariance matrix specification for subject and for items. I suggest here that the recommendation should not be to fit maximal models, the recommendation should be to run high power studies.
I released a simulation on this blog some time ago arguing that the correlation parameters are pretty meaningless. Dale Barr and Jake Westfall replied to my post, raising some interesting points. I have to agree with Dale's point that we should reflect the design of the experiment in the analysis; after all, our goal is to specify how we think the data were generated. But my main point is that given the fact that the culture in psycholinguistics is to run low power studies (we routinely publish null results with low power studies and present them as positive findings), fitting maximal models without asking oneself whether the various parameters are reasonably estimable will lead us to miss effects.
For me, the only useful recommendation to psycholinguists should be to run high power studies.
Consider two cases:
1. Run a low power study (the norm in psycholinguistics) where the null hypothesis is false.
If you blindly fit a maximal model, you are going to miss detecting the effect more often compared to when you fit a minimal model (varying intercepts only). For my specific example below, the proportions of false negatives is 38% (maximal) vs 9% (minimal).
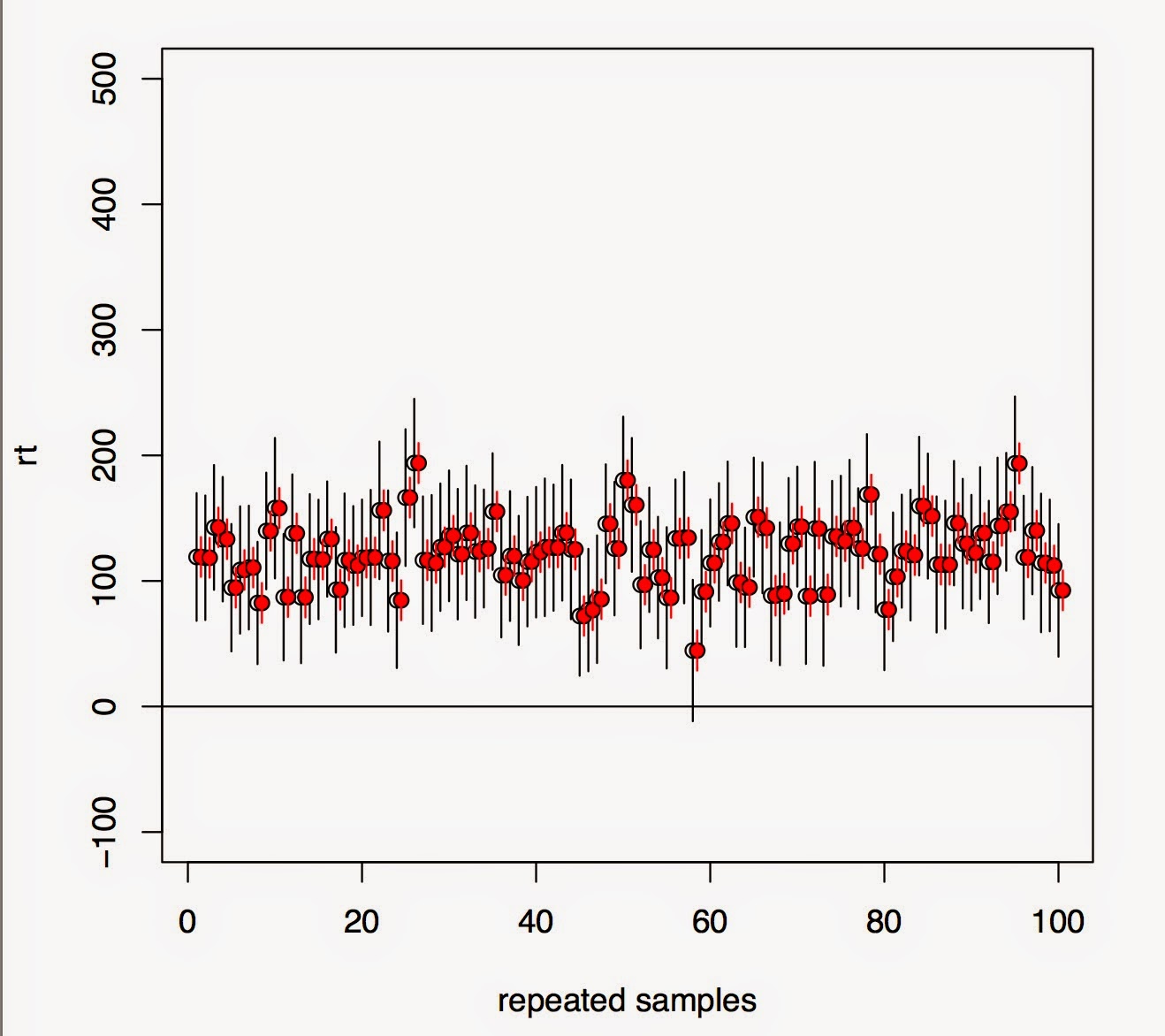
In the top figure, we see that under repeated sampling, lmer is failing to estimate the true correlations for items (it's doing a better job for subjects because there is more data for subjects). Even though these are nuisance parameters, trying to estimate them for items in this dataset is a meaningless exercise (and the fact that the parameterization is going to influence the correlations is not the key issue here---that decision is made based on the hypotheses to be tested).
The lower figure shows that under repeated sampling, the effect (\mu is positive here, see my earlier post for details) is being missed much more often with a maximal model (black lines, 95% CIs) than with a varying intercepts model (red lines). The difference is in the miss probability is 38% (maximal) vs 9% (minimal).
2. Run a high power study.
Now, it doesn't really matter whether you fit a maximal model or not. You're going to detect the effect either way. The upper plot shows that under repeated sampling, lmer will tend to detect the true correlations correctly. The lower plot shows that in almost 100% of the cases, the effect is detected regardless of whether we fit a maximal model (black lines) or not (red lines).
My conclusion is that if we want to send a message regarding best practice to psycholinguistics, it should not be to fit maximal models. It should be to run high power studies. To borrow a phrase from Andrew Gelman's blog (or from Rob Weiss's), if you are running low power studies, you are leaving money on the table.
Here's my code to back up what I'm saying here. I'm happy to be corrected!
https://gist.github.com/vasishth/42e3254c9a97cbacd490
I released a simulation on this blog some time ago arguing that the correlation parameters are pretty meaningless. Dale Barr and Jake Westfall replied to my post, raising some interesting points. I have to agree with Dale's point that we should reflect the design of the experiment in the analysis; after all, our goal is to specify how we think the data were generated. But my main point is that given the fact that the culture in psycholinguistics is to run low power studies (we routinely publish null results with low power studies and present them as positive findings), fitting maximal models without asking oneself whether the various parameters are reasonably estimable will lead us to miss effects.
For me, the only useful recommendation to psycholinguists should be to run high power studies.
Consider two cases:
1. Run a low power study (the norm in psycholinguistics) where the null hypothesis is false.
If you blindly fit a maximal model, you are going to miss detecting the effect more often compared to when you fit a minimal model (varying intercepts only). For my specific example below, the proportions of false negatives is 38% (maximal) vs 9% (minimal).
In the top figure, we see that under repeated sampling, lmer is failing to estimate the true correlations for items (it's doing a better job for subjects because there is more data for subjects). Even though these are nuisance parameters, trying to estimate them for items in this dataset is a meaningless exercise (and the fact that the parameterization is going to influence the correlations is not the key issue here---that decision is made based on the hypotheses to be tested).
The lower figure shows that under repeated sampling, the effect (\mu is positive here, see my earlier post for details) is being missed much more often with a maximal model (black lines, 95% CIs) than with a varying intercepts model (red lines). The difference is in the miss probability is 38% (maximal) vs 9% (minimal).
2. Run a high power study.
Now, it doesn't really matter whether you fit a maximal model or not. You're going to detect the effect either way. The upper plot shows that under repeated sampling, lmer will tend to detect the true correlations correctly. The lower plot shows that in almost 100% of the cases, the effect is detected regardless of whether we fit a maximal model (black lines) or not (red lines).
My conclusion is that if we want to send a message regarding best practice to psycholinguistics, it should not be to fit maximal models. It should be to run high power studies. To borrow a phrase from Andrew Gelman's blog (or from Rob Weiss's), if you are running low power studies, you are leaving money on the table.
Here's my code to back up what I'm saying here. I'm happy to be corrected!
https://gist.github.com/vasishth/42e3254c9a97cbacd490
Saturday, November 22, 2014
Simulating scientists doing experiments
Following a discussion on Gelman's blog, I was playing around with simulating scientists looking for significant effects. Suppose each of 1000 scientists run 200 experiments in their lifetime, and suppose that 20% of the experiments are such that the null is true. Assume a low power experiment (standard in psycholinguistics; eyetracking studies even in journals like JML can easily have something like 20 subjects). E.g., with a sample size of 1000, delta of 2, and sd of 50, we have power around 15%. We will add the stringent condition that the scientist has to get one replication of a significant effect before they publish it.
What is the proportion of scientists that will publish at least one false positive in their lifetime? That was the question. Here's my simulation. You can increase the effect_size to 10 from 2 to see what happens in high power situations.
Comments and/or corrections are welcome.
What is the proportion of scientists that will publish at least one false positive in their lifetime? That was the question. Here's my simulation. You can increase the effect_size to 10 from 2 to see what happens in high power situations.
Comments and/or corrections are welcome.
Saturday, August 23, 2014
An adverse consequence of fitting "maximal" linear mixed models
 |
| Distribution of intercept-slope correlation estimates with 37 subjects, 15 items |
 |
| Distribution of intercept-slope correlation estimates with 50 subjects, 30 items |
Let's create a repeated measures data-set that has two conditions (we want to keep this example simple), and the following underlying generative distribution, which is estimated from the Gibson and Wu 2012 (Language and Cognitive Processes) data-set. The dependent variable is reading time (rt).
\begin{equation}\label{eq:ranslp2}
rt_{i} = \beta_0 + u_{0j} + w_{0k} + (\beta_1 + u_{1j} + w_{1k}) \hbox{x}_i + \epsilon_i
\end{equation}
\begin{equation}
\begin{pmatrix}
u_{0j} \\
u_{1j}
\end{pmatrix}
\sim
N\left(
\begin{pmatrix}
0 \\
0
\end{pmatrix},
\Sigma_{u}
\right)
\quad
\begin{pmatrix}
w_{0k} \\
w_{1k} \\
\end{pmatrix}
\sim
N \left(
\begin{pmatrix}
0 \\
0
\end{pmatrix},
\Sigma_{w}
\right)
\end{equation}
\begin{equation}\label{eq:sigmau}
\Sigma_u =
\left[ \begin{array}{cc}
\sigma_{\mathrm{u0}}^2 & \rho_u \, \sigma_{u0} \sigma_{u1} \\
\rho_u \, \sigma_{u0} \sigma_{u1} & \sigma_{u1}^2\end{array} \right]
\end{equation}
\begin{equation}\label{eq:sigmaw}
\Sigma_w =
\left[ \begin{array}{cc}
\sigma_{\mathrm{w0}}^2 & \rho_w \, \sigma_{w0} \sigma_{w1} \\
\rho_w \, \sigma_{w0} \sigma_{w1} & \sigma_{w1}^2\end{array} \right]
\end{equation}
\begin{equation}
\epsilon_i \sim N(0,\sigma^2)
\end{equation}
One difference from the Gibson and Wu data-set is that each subject is assumed to see each instance of each item (like in the old days of ERP research), but nothing hinges on this simplification; the results presented will hold regardless of whether we do a Latin square or not (I tested this).
The parameters and sample sizes are assumed to have the following values:
* $\beta_1$=487
* $\beta_2$= 61.5
* $\sigma$=544
* $\sigma_{u0}$=160
* $\sigma_{u1}$=195
* $\sigma_{w0}$=154
* $\sigma_{w1}$=142
* $\rho_u=\rho_w$=0.6
* 37 subjects
* 15 items
Next, we generate data 100 times using the above parameter and model specification, and estimate (from lmer) the parameters each time. With the kind of sample size we have above, a maximal model does a terrible job of estimating the correlation parameters $\rho_u=\rho_w$=0.6.
However, if we generate data 100 times using 50 subjects instead of 37, and 30 items instead of 15, lmer is able to estimate the correlations reasonably well.
In both cases we fit ''maximal'' models; in the first case, it makes no sense to fit a "maximal" model because the correlation estimates tend to be over-estimated. The classical method (the generalized likelihood ratio test (the anova function in lme4) to find the ''best'' model) for determining which model is appropriate is discussed in the Pinheiro and Bates book, and would lead us to adopt a simpler model in the first case.
Douglas Bates himself has something to say on this topic:
https://stat.ethz.ch/pipermail/r-sig-mixed-models/2014q3/022509.html
As Bates puts it:
"Estimation of variance and covariance components requires a large number of groups. It is important to realize this. It is also important to realize that in most cases you are not terribly interested in precise estimates of variance components. Sometimes you are but a substantial portion of the time you are using random effects to model subject-to-subject variability, etc. and if the data don't provide sufficient subject-to-subject variability to support the model then drop down to a simpler model. "
Here is the code I used:
Tuesday, December 17, 2013
lmer vs Stan for a somewhat involved dataset.
Here is a comparison of lmer vs Stan output on a mildly complicated dataset from a psychology expt. (Kliegl et al 2011). The data are here: https://www.dropbox.com/s/pwuz1g7rtwy17p1/KWDYZ_test.rda.
The data and paper available from: http://openscience.uni-leipzig.de/index.php/mr2
I should say that datasets from psychology and psycholinguistic can be much more complicated than this. So this was only a modest test of Stan.
The basic result is that I was able to recover in Stan the parameter estimates (fixed effects) that were primarily of interest, compared to the lmer output. The sds of the variance components all come out pretty much the same in Stan vs lmer. The correlations estimated in Stan are much smaller than lmer, but this is normal: the bayesian models seem to be more conservative when it comes to estimating correlations between random effects.
Traceplots are here: https://www.dropbox.com/s/91xhk7ywpvh9q24/traceplotkliegl2011.pdf
They look generally fine to me.
One very important fact about lmer vs Stan is that lmer took 23 seconds to return an answer, but Stan took 18,814 seconds (about 5 hours), running 500 iterations and 2 chains.
One caveat is that I do have to try to figure out how to speed up Stan so that we get the best performance out of it that is possible.
The data and paper available from: http://openscience.uni-leipzig.de/index.php/mr2
I should say that datasets from psychology and psycholinguistic can be much more complicated than this. So this was only a modest test of Stan.
The basic result is that I was able to recover in Stan the parameter estimates (fixed effects) that were primarily of interest, compared to the lmer output. The sds of the variance components all come out pretty much the same in Stan vs lmer. The correlations estimated in Stan are much smaller than lmer, but this is normal: the bayesian models seem to be more conservative when it comes to estimating correlations between random effects.
Traceplots are here: https://www.dropbox.com/s/91xhk7ywpvh9q24/traceplotkliegl2011.pdf
They look generally fine to me.
One very important fact about lmer vs Stan is that lmer took 23 seconds to return an answer, but Stan took 18,814 seconds (about 5 hours), running 500 iterations and 2 chains.
One caveat is that I do have to try to figure out how to speed up Stan so that we get the best performance out of it that is possible.
Monday, December 16, 2013
The most common linear mixed models in psycholinguistics, using JAGS and Stan
As part of my course in bayesian data analysis, I have put up some common linear mixed models that we fit in psycholinguistics. These are written in JAGS and Stan. Comments and suggestions for improvement are most welcome.
Code: http://www.ling.uni-potsdam.de/~vasishth/lmmexamplecode.txt
Data: http://www.ling.uni-potsdam.de/~vasishth/data/gibsonwu2012data.txt
Code: http://www.ling.uni-potsdam.de/~vasishth/lmmexamplecode.txt
Data: http://www.ling.uni-potsdam.de/~vasishth/data/gibsonwu2012data.txt
Tuesday, October 08, 2013
New course on bayesian data analysis for psycholinguistics
I decided to teach a basic course on bayesian data analysis with a focus on psycholinguistics. Here is the course website (below). How could this possibly be a bad idea!
http://www.ling.uni-potsdam.de/~vasishth/advanceddataanalysis.html
http://www.ling.uni-potsdam.de/~vasishth/advanceddataanalysis.html
Friday, March 15, 2013
How are the random effects (BLUPs) `predicted' in linear mixed models?
In linear mixed models, we fit models like these (the Ware-Laird formulation--see Pinheiro and Bates 2000, for example):
\begin{equation}
Y = X\beta + Zu + \epsilon
\end{equation}
Let $u\sim N(0,\sigma_u^2)$, and this is independent from $\epsilon\sim N(0,\sigma^2)$.
Given $Y$, the ``minimum mean square error predictor'' of $u$ is the conditional expectation:
\begin{equation}
\hat{u} = E(u\mid Y)
\end{equation}
We can find $E(u\mid Y)$ as follows. We write the joint distribution of $Y$ and $u$ as:
\begin{equation}
\begin{pmatrix}
Y \\
u
\end{pmatrix}
=
N\left(
\begin{pmatrix}
X\beta\\
0
\end{pmatrix},
\begin{pmatrix}
V_Y & C_{Y,u}\\
C_{u,Y} & V_u \\
\end{pmatrix}
\right)
\end{equation}
$V_Y, C_{Y,u}, C_{u,Y}, V_u$ are the various variance-covariance matrices.
It is a fact (need to track this down) that
\begin{equation}
u\mid Y \sim N(C_{u,Y}V_Y^{-1}(Y-X\beta)),
Y_u - C_{u,Y} V_Y^{-1} C_{Y,u})
\end{equation}
This apparently allows you to derive the BLUPs:
\begin{equation}
\hat{u}= C_{u,Y}V_Y^{-1}(Y-X\beta))
\end{equation}
Substituting $\hat{\beta}$ for $\beta$, we get:
\begin{equation}
BLUP(u)= \hat{u}(\hat{\beta})C_{u,Y}V_Y^{-1}(Y-X\hat{\beta}))
\end{equation}
Here is a working example:
Correlations of fixed effects in linear mixed models
Ever wondered what those correlations are in a linear mixed model? For example:
The estimated correlation between $\hat{\beta}_1$ and $\hat{\beta}_2$ is $0.988$. Note that
$\hat{\beta}_1 = (Y_{1,1} + Y_{2,1} + \dots + Y_{10,1})/10=10.360$
and
$\hat{\beta}_2 = (Y_{1,2} + Y_{2,2} + \dots + Y_{10,2})/10 = 11.040$
From this we can recover the correlation $0.988$ as follows:
By comparison, in the linear model version of the above:
because $Var(\hat{\beta}) = \hat{\sigma}^2 (X^T X)^{-1}$.
Wednesday, January 23, 2013
Linear models summary sheet
As part of my long slog towards statistical understanding, I started making notes on the very specific topic of linear models. The details are tricky and hard to keep in mind, and it is difficult to go back and forth between books and notes to try to review them. So I tried to summarize the basic ideas into a few pages (the summary sheet is not yet complete).
It's not quite a cheat sheet, so I call it a summary sheet.
Here is the current version:
https://github.com/vasishth/StatisticsNotes
Needless to say (although I feel compelled to so it), the document is highly derivative of lecture notes I've been reading. Corrections and comments and/or suggestions for improvement are most welcome.
It's not quite a cheat sheet, so I call it a summary sheet.
Here is the current version:
https://github.com/vasishth/StatisticsNotes
Needless to say (although I feel compelled to so it), the document is highly derivative of lecture notes I've been reading. Corrections and comments and/or suggestions for improvement are most welcome.
Saturday, March 03, 2012
Cauchy and determinants: when life was simple
" In Cauchy's day, when life was simple and matrices were small, determinants played a major role in analytic geometry and other parts of mathematics."
Lay, p. 202 [Linear Algebra and its Applications, 3rd Edition (Update)]
Lay, p. 202 [Linear Algebra and its Applications, 3rd Edition (Update)]
Saturday, February 04, 2012
Alpha values
Recently seen quote on Gelman's blog:
“No scientific worker has a fixed level of significance at which from year to year, and in all circumstances, he rejects hypotheses; he rather gives his mind to each particular case in the light of his evidence and his ideas.”
(Ronald A. Fisher, 1956, p. 42)
Also read about mindless statistics here: http://people.umass.edu/~bioep740/yr2009/topics/Gigerenzer-jSoc-Econ-1994.pdf
“No scientific worker has a fixed level of significance at which from year to year, and in all circumstances, he rejects hypotheses; he rather gives his mind to each particular case in the light of his evidence and his ideas.”
(Ronald A. Fisher, 1956, p. 42)
Also read about mindless statistics here: http://people.umass.edu/~bioep740/yr2009/topics/Gigerenzer-jSoc-Econ-1994.pdf
Thursday, January 26, 2012
How to append R code in appendix using Sweave
In the statistics course I'm doing, the solutions to assignments have R code, but the instructor doesn't want to see them in the main text but rather in an appendix. Here's apparently how to do that without copying and pasting the code into an appendix (I got this nifty example from here):
\begin{appendix}
\section{Appendix A}
\subsection{R session information}
<<SessionInforamtaion,echo=F,eval=T,results=tex>>=
toLatex(sessionInfo())
@
\subsection{The simulation's source code}
<>=
Stangle(file.path("Projectpath","RnwFile.Rnw"))
SourceCode <- readLines(file.path("Projectpath","Codefile.R"))
writeLines(SourceCode)
@
\end{appendix} Thursday, December 01, 2011
Review of Distance Course: Graduate Certificate in Statistics offered at Sheffield [completed: 3 June 2012]
Recently, on Andrew Gelman's blog there was a discussion about how to get yourself a statistics education (presumably without going through the whole process of becoming a professional statistician). Here's the discussion on Gelman's blog, with lots of suggestions on how to achieve this goal.
This was the kind of problem that motivated me to look for a full course of study that would give me the background that's missing.
In September 2011, I started a graduate certificate in statistics, at Sheffield (my wife's alma mater, coincidentally). preparatory course, which gets you ready to start an MSc in statistics. It's a nine-month affair with three courses (Math, Probability, Statistics) which are taught more or less in parallel (they cleverly stagger the assignment submissions so that one is only working on one of the three at any one time). The course guide says it's a time commitment of 15 hours a week, which seems amazingly little (imagine that you devote the last three hours of your day to working on something like this---you could easily exceed 15 hours a week). But it's a realistic number; I think I spent about that much time every week on it. Occasionally I have spent more (when I ran into trouble).
Short version: the course is *excellent*. I wish I had done this years ago. But I would recommend it only to people who are really willing to sweat it out. You have to be able to do your own research when you need more detail on a particular topic. The instructors can be helpful, but the interaction is through a mailing list, and response lag can be several days. Quite often, though, the instructors' responses did not help me much and I had to do my own research. I think the main positive aspect of this course is that it spells out what you need to know and in what order. If you look at the vast space that is calculus, linear algebra, probability theory, and statistics, such guidance is extremely helpful.
Long version:
Preparation for the course: I wish I had reviewed permutations and combinations, and trigonometry before starting the course. I found it the hardest to recall these things while working through the course. I would recommend the following sites for trig:
http://en.wikipedia.org/wiki/Trig_identities
http://www.mecmath.net/trig/
For permutations and combinations, this is badly formatted but it could be useful: http://www.bmlc.ca/PureMath30/Pure%20Math%2030%20-%20Permutations%20and%20Combinations.html
The courses:
There are three modules:
1. Math: http://maths.dept.shef.ac.uk/maths/module_info.php?id=985
2. Probability: http://maths.dept.shef.ac.uk/maths/module_info.php?id=987
3. Statistics: http://maths.dept.shef.ac.uk/maths/module_info.php?id=990
The assignments:
Each assignment I did (a total of 18 to be assigned by the time the course ends; only the last 15 are graded) took a lot of time, and if you are typesetting the submission in LaTeX, you should expect a full day to be devoted to that (at least). I gave up typesetting---to my great regret---in the math and probability courses towards the end of the course because it takes too long.
Most of the questions directly use knowledge that was recently covered in the course, but some of the questions require thought and insight (which takes time).
I wish the assignments had been prepared with greater attention to precision in writing. A couple of times I had a hard time trying to figure out what precisely was meant, and judging from the others' questions, I was not the only one. I should say that it's inherently hard to write good assignments (my own students sometimes suffer due to lack of clarity in assignments I sent for them).
The grading is tough, but I kind of like it that the graders are so reluctant to give a point. You have to respect them for that. When I saw how they grade, I felt a bit ashamed that I am so soft on my students in Potsdam. These guys are really hard-nosed. I guess I've gone soft after eight years in a soft-skills (no pun intended) oriented linguistics department. Computer science and math at Ohio State was about as strict, although the math guys at OSU were a bit more relaxed, but only a bit.
My grades so far are as below (percentages). This excludes the first assignments; they do not count for the final grade. In general, these assignments count for 20% of the final grade. You have to get minimum 65% overall in the final grade (after the exams in June 2012) to be allowed to continue on to the MSc.
Average score of all homework assignments: 84.87%
Final exam scores: unknown.
Mathematics: mean score 93.4%
Assignment-1: 100%
## Notes: I was pleasantly surprised to get this grade, but I do admit the problems were not too hard. The hardest part of this course is not the math but the probability theory.
Assignment-2: 97%
## Made a stupid mistake. Don't ask.
Assignment-3: 81%
## Here, I lost a lot of points for not generalizing my solution for a particular proof, and I made a stupid mistake in a partial derivative computation (forgot to treat y as a constant when differentiating with respect to x) that caused a snowball-effect error in the final answer, and I thought that level curves are three-dimensional and plotted them as such. All errors could have been avoided if I had carefully re-read what I'd done, but there was no time (this was also the only submission so far which was not typeset, perhaps another reason why I didn't notice the errors---when typesetting I usually discover a lot of mistakes in my solutions, esp. since I check my solutions at that stage with R or a computer algebra system like yacas).
Assignment-4: 100%
## Several people got 100% I believe. It was relatively easy because it was about really basic linear algebra mostly.
Assignment-5: 89%
## The first quartile was 83% it seems, and the third was 97%, so I clearly did not do well. I made some amazingly stupid arithmetic errors (like putting in a negative sign where there was supposed to be none), and it just adds up (or subtracts off). I had a hard time with one problem involving the computation of eigenvectors, and with a change of variables problem. I also made a stupid mistake in a double integral (miscopying one line onto the next, how dumb is that). All costly mistakes.
Probability: mean score 78.8%
Assignment-1: 76%
## Notes: I did relatively badly in the first assignment because I reversed a couple of signs accidentally, and because I didn't leave enough time for working on the assignment. I lost a lot of points on a stupid and mindless exercise involving reading numbers off of a binomial probability table --- shame on me.
Assignment-2: 96%
## Notes: The instructor cut 4 percentage points when I said that a particular distribution (I discovered later that this was the Cauchy distribution) had expectation infinity. He said I should have said "expectation does not exist." He's right, of course, but it was a painful loss, given that I didn't know at that time that infinity cannot be considered to exist in this particular context. That's a painful lesson.
Assignment-3: 70%
## Notes: I lost a lot of points for small things, like not defining a random variable X before I mention it (I thought it was clear from context, but I see that technically one has to define everything---God, I am out of touch with formal proofs and such like). The moral was that I have to write a lot more precisely. Perhaps there will be an improvement in the next submission's grades.
Assignment-4: 88%
## I made lots of small errors, and they add up.
Assignment-5: 64%
## Very hard assignment, done in a hurry because exams were imminent. Everyone's grades suffered. 64% was above average.
Statistics: mean score 82.4%
Assignment-1: 84%
Assignment-2: 82%
### It is amazing that the one thing I thought I could do---data analysis---is
## giving me the most trouble in this course. The grading is pretty harsh; for example, if you report a p=0.30 and don't say explicitly that you reject the null hypothesis, you lose points. I did make some horrible mistakes in this assignment though, so I do deserve losing some marks.
Assignment-3: 88%
## I got almost everything right, but I lost most of those 12% points for not defining \mu whenever I set up the null hypothesis. I was a bit crestfallen that most of those 12% points were cut for a repeated failure to define \mu (I felt it was clear from context what mu was in each case...).
Assignment-4: 84%
## I'm actually surprised I do so badly in the stats segment, compared to the other ones (math and probability).
Assignment-5: 74%
## Also done in a hurry. I don't know how the others did.
The textbooks:
One minor gripe I have in the course is some of the textbooks assigned. I think the course designers should probably invest some time into building complete course-specific lecture notes. Sometimes they do provide lectures notes, and these are great (my only complaint is that the authors don't believe in page numbers, which can be a real hassle if you print out the material and accidentally drop them on the floor). But that said, I realize that producing customized lecture notes is a major undertaking and I don't blame them for relying on existing books.
The math textbook is by Gilbert and Jordan, Guide$^2$ Mathematical Methods. The title is a bit strange, I mean the 2 instead of "to" (although the authors cannot be blamed for this naming decision---apparently Macmillan has a Guide 2... series). The book has one positive aspect: it covers the relevant material in the sense that it goes through the topics. So, for someone like me, who doesn't know exactly what I need to know as background to read more advanced textbooks on statistics, this is a good extended listing of the things I should know (or recall from high school). This is all good. What makes the reader's life hard are the super-terse proofs/solutions to exercises, and the large number of typos (especially in the solutions). The course organizers released a list of typos for the book at the start of the course, but there are even more typos than in the errata. The notation can also be sloppy and the reader has to be careful (e.g., at one point they write F-p, where F are the *names* of a function; what they meant was F(x)-p(x)).
An example of the terseness is the proof that the limit of sin(x)/x when x approaches 0 is 1. I had no idea where that proof was going until I watched Strang's online lecture (MIT open courseware). After watching Strang's lecture, I was able to unpack the proof myself, but I doubt that it could be done easily by just working through it (are proofs meant to be hard work to unpack? Read the Salas et al book on Calculus to see that the answer may be no). Gilbert and Jordan should read Knuth's book on writing mathematics. I would recommend Strang's lectures, and Calculus by Salas, Hille and Etgen (I have the 9th Edition); this last book really nailed it for me. This book has the smoothness and feel of Cormen, Rivest et al on Algorithms.
The probability theory book (Ross, A First Course in Probability) is OK in that it covers all the points. But it has the irritating property that each definition is followed by half a dozen totally unrelated examples. This in itself is not bad, but the examples are SCARY. I'm not sure I need to see the toughest applications of the latest idea learnt right away. After a bit of reading this sort of teaching-by-example at least this reader just gets depressed (there is no way I would have worked out those example answers myself after just reading the definitions provided immediately earlier). I found the online book by Jay Kerns much, much more useful for the present course---the course organizers should consider switching to that or at least assigning it alongside Ross, with some warnings to not get intimidated by Ross' style. Here is an excellent review of the Ross book on amazon that pretty much summarizes the main problems in the book.
There is an accompanying book on probability (by Freund, but authors are Miller and Miller) which is a straightforward and formal introduction to mathematical statistics; I like that more. It's part of the statistics course, not the probability course.
The statistics textbook is by Moore, McCabe and someone else, is absolutely terrible (apparently I'm not the only one complaining; see here). The book seems to be written for first year undergrads in statistics (nothing wrong with that of course, but this graduate certificate has a different audience). The large number of disconnected and silly examples (for example, for planned experiments vs observational studies) following every new concept lead to a feeling of total disorientation. There is also a painful attempt to make the book relevant to the modern user: examples about cell phones and iPhone Apps abound, presumably to draw in the young reader's eyes away from the cell phone as they read. The book could be a lot slimmer if all the extraneous junk is removed and they just stick to the facts presented.
There are so many really good books on introductory statistics using R (e.g., in the Use R! series); I wish they had used one of them. As it is, you have to be either real good at R, or be able to quickly get on board with R, if you want to do this course. Since the course is completely based on R, it is absolutely wonderful for me, but several of the students went into a state of blind panic (for example, a beginner often cannot easily figure out how to find out how to change a directory within R---in my own courses at Potsdam, I think we spend about 90 minutes just getting them used to the interface). Using an R-based book for introductory statistics would have been much better than Moore et al's. I have to admit though that I cannot name an alternative to Moore et al's right away that covers exactly the same material. I would like the book a lot more if there was a version for grown-up people: no photos of people holding cell phones, no extended and long-drawn out examples, just the facts.
I have concluded that the linear algebra books assigned in this course suck. They never tell you why one should care about such and such fact, and they overload the book with proofs. Also, linear algebraists apparently think they have a great sense of humor. Both Allenby and Lay, the former a bit more, deliver lots of intended-to-be-funny comments followed by an exclamation point. Lay can be very clear, though.
If anyone wants their first contact with linear algebra to be not painful, they should read Leonard Evens' excellent online book, which he has the generosity to release for free: http://www.math.northwestern.edu/~len/LinAlg/index.html. (I find it embarrassing that he wrote such a beautiful book and released it for free, whereas I have Springer charge for mine. Never again.) On the other hand, all these people writing expensive linear algebra texts should also be feeling a bit embarrassed to be out-performed by a free textbook (my super-expensive Lay textbook doesn't even have all the pages, some 10-20 pages are simply not there; the publishers apparently screwed up, and the table of contents page numbering bears no relationship to the actual numbers, so the table of contents is not only useless but actually misleading). Evens released his book with essentially no restrictions, with the source code. I really admire that.
I also found Gilbert Strang's book and online lectures on matrix algebra very cool. Denis Auroux's lectures are also quite amazing.
One thing worth noting about this course---I was not prepared for this---is that the last five lectures (out of 40) in each module (math, probability, and statistics) are the most demanding. I really had to sweat over this part of the course in a way I never had to for the earlier parts. Part of the reason is that these last five lectures deploy a lot of the material you learnt in the last 35 lectures, and obviously I don't have everything in my head and easily retrievable, so it was hard going to try to recall, for example, how to differentiate this or that function.
The concepts involving the method of moments, maximum likelihood estimates, likelihood ratio tests (in statistics); linear algebra, double integrals using polar coordinates and change of variables (math), and such like things were really overwhelming as they came in all at once towards the end. It doesn't help that the textbooks give pretty obscure discussions about this; in this part of the course I really had to google my way through these topics, by watching MIT Opencourseware lectures and reading dumbed down versions of these topics. What I missed the most in the textbooks was the why: why are we doing this, in the sense that where is this going? These online resources explain this mysterious aspect very well. Normally, it's almost anti-intellectual to ask a question like "why are we learning this?", but here, I really needed to know where I am going when I do an LRT or use the Neyman-Pearson Lemma, for example, or why a null space is called a null space (Evens answers that question). What's most remarkable though is the sheer range of resources available on the web to answer these questions. A lot of people spent a lot of their valuable time helping out poor suckers like me, who just don't get it. MIT Opencourseware is to be congratulated for releasing (for free) videos of so many important lectures on math and linear algebra.
Some other minor gripes about the course
1. In one of the pages of Ross' book (our assigned text), he writes "...if \sigma=\infty....". Now, in one of the probability theory assignments (Assignment 3) I lost four percentage points for saying that E[X]=\infty. I lost marks because I should have written, "the mean does not exist." This is correct, you do have to write exactly that. But when I pointed out that Ross makes the same mistake, I was told that that was a slight abuse of notation but it's fine. Seems like if a statistician writes something incorrectly, it's OK, but not if a student writes the same thing (maybe this makes sense, if you think about it). If I had seen Ross' statement before writing my assignment solution, would I still deserve to lose 4 percentage points? I found this double standard irritating. I have to admit that I am just whining about losing those four points (and these four points contribute almost nothing to the final grade, as homework assignments count for only 20 percent of the final grade), and so I'm perhaps just being a sore loser.
2. The statement of some of the probability theory problems in the homework assignments was very unclear. It's hard to write unambiguously, that's understandable; but I would have expected clearly worded problems. Even worse, the clarifications one got after asking for more detail led to so much confusion among us students (at one point the lecturer was contradicting an earlier statement) that in one case we just gave up and went with our interpretation, which seemed according to the messages from lecturer to be wrong (I will report later if our interpretation got full marks or not; it turns out my own interpretation was correct, I got full marks). I was not the only one facing this problem; there was a flurry of unhappiness about the question. This is true for occasional other assignments (I would say in maybe 2% of all cases there was some ambiguity, so it's definitely not a serious issue). For example, in one of the stats assignments we have a garden-path that fooled a student:
"Compare this with what happens if you first include the interaction with the residual..."
The author of this assignment intended a non-local attachment of the prepositional phrase "with the residual" to "compare", not to "interaction". The student wanted to know how to compute "the interaction with the residual". A more common class of error is scope ambiguities (usually fatal ones). Maybe mathematicians and statisticians need to study formal semantics and syntax!
3. Too often, the response to clarification questions can take up to a week or more; this is simply too long a period for a course moving as fast as this one. In some cases, I just had to go with what I understood. This isn't too serious; one often leaves a course with many questions unanswered, and after all this course is just a prep course for the real thing, the MSc. But it could be optimized by asking the lecturers to check the message board at least once a day or every other day.
Final exams
The final exams were designed with the following assumptions in mind: (a) you are not expected to finish them on time unless you could immediately solve every problem without thinking much about it, or thinking extremely fast, (b) you can compute on the calculator extremely fast, (c) you have everything on your fingertips (the exam is open book, but one does not really have time to look things up). I think I'll be lucky if I make the 65% "passing" grade (passing in the sense that one can proceed to the MSc).
One mistake I made was that I should have regularly reviewed every single topic incrementally as the course progressed, and I should have kept doing exercises on old topics (e.g., integration techniques), so that I would not forget details from a few months ago. Next time I will be a lot more systematic in doing revision. Mathematicians are not kidding when they say you have to practice every single day; it's no different from playing the violin.
Conclusion
Overall, a thumbs-up. This is a course every non-statistician who needs to work with data should take. Even in these few months I learnt a lot of interesting and even downright cool things (mostly in the math segment, but also in probability theory).
The big advantages of doing this kind of structured course are that:
- you have to solve problems on a daily basis in order to the get the assignments done on time, and someone carefully checks your work. If you try to read books on topics that are specifically relevant to you, like Gelman recommends, you are not going to get that quality of feedback (no, not even with a solutions manual).
- you can ask a statistician questions that come up as you read or work on real problems that affect your own life, and they will often take the time to answer them fully. This is virtually impossible if you just try to talk to a random statistician (generally, they either heap scorn on you, or give a rambling answer that doesn't really answer the question, because they just don't want to pay attention long enough to try to understand the problem---not that I blame them for that; why should they care what your problem is?).
Some of the material I consulted while doing this course (incomplete):
1. On writing math
2. Kerns' book on probability
3. Grinstead and Snell on probability
4. Salas et al Calculus
5. Spivak Calculus
6. MIT Open courseware (Strang, Auroux on calculus and linear algebra)
I consulted many other books, I will put a list online one of these days.
Software I used in this course:
1. R
2. Yacas (with Ryacas and without), to check my answers, arrived at analytically.
3. Mathematica to check my solve-for-theta type of solutions.
4. Matlab (I forgot why I used Matlab instead of Mathematica, but I did).
What next?
So, now I know almost everything they taught in this course. This is supposed to be (almost?) equivalent to an undergrad degree in statistics, but I doubt that, because one cannot learn in nine months what others have spent three years learning. But I do know enough to move on to more advanced texts. After some asking around (Sheffield instructors) and doing some research, I concluded that I need to read two books completely:
1. Salas et al on Calculus; Strang and Auroux's lectures on calculus.
2. Shayle Searle's "Matrix Algebra useful for Statistics" (the graduate certificate teaches you almost everything in this book, but it's a nice review nonetheless, and talks about some details not covered in the course)
3. James Gentle on Matrix Algebra. Gentle's book seems to be a classic, but it's hard going so be prepared to read slowly.
4. Strang's lectures on calculus and matrix algebra (Strang's book on Matrix Algebra is also a pleasure to read, you can feel his personality shine through his words).
This material will cover pretty much all the math I would need for a good understanding of statistical theory. This is an incomplete list, of course, and it's based on my own conclusions about what is needed, so it may not even be the right list.
This was the kind of problem that motivated me to look for a full course of study that would give me the background that's missing.
In September 2011, I started a graduate certificate in statistics, at Sheffield (my wife's alma mater, coincidentally). preparatory course, which gets you ready to start an MSc in statistics. It's a nine-month affair with three courses (Math, Probability, Statistics) which are taught more or less in parallel (they cleverly stagger the assignment submissions so that one is only working on one of the three at any one time). The course guide says it's a time commitment of 15 hours a week, which seems amazingly little (imagine that you devote the last three hours of your day to working on something like this---you could easily exceed 15 hours a week). But it's a realistic number; I think I spent about that much time every week on it. Occasionally I have spent more (when I ran into trouble).
Short version: the course is *excellent*. I wish I had done this years ago. But I would recommend it only to people who are really willing to sweat it out. You have to be able to do your own research when you need more detail on a particular topic. The instructors can be helpful, but the interaction is through a mailing list, and response lag can be several days. Quite often, though, the instructors' responses did not help me much and I had to do my own research. I think the main positive aspect of this course is that it spells out what you need to know and in what order. If you look at the vast space that is calculus, linear algebra, probability theory, and statistics, such guidance is extremely helpful.
Long version:
Preparation for the course: I wish I had reviewed permutations and combinations, and trigonometry before starting the course. I found it the hardest to recall these things while working through the course. I would recommend the following sites for trig:
http://en.wikipedia.org/wiki/Trig_identities
http://www.mecmath.net/trig/
For permutations and combinations, this is badly formatted but it could be useful: http://www.bmlc.ca/PureMath30/Pure%20Math%2030%20-%20Permutations%20and%20Combinations.html
The courses:
There are three modules:
1. Math: http://maths.dept.shef.ac.uk/maths/module_info.php?id=985
2. Probability: http://maths.dept.shef.ac.uk/maths/module_info.php?id=987
3. Statistics: http://maths.dept.shef.ac.uk/maths/module_info.php?id=990
The assignments:
Each assignment I did (a total of 18 to be assigned by the time the course ends; only the last 15 are graded) took a lot of time, and if you are typesetting the submission in LaTeX, you should expect a full day to be devoted to that (at least). I gave up typesetting---to my great regret---in the math and probability courses towards the end of the course because it takes too long.
Most of the questions directly use knowledge that was recently covered in the course, but some of the questions require thought and insight (which takes time).
I wish the assignments had been prepared with greater attention to precision in writing. A couple of times I had a hard time trying to figure out what precisely was meant, and judging from the others' questions, I was not the only one. I should say that it's inherently hard to write good assignments (my own students sometimes suffer due to lack of clarity in assignments I sent for them).
The grading is tough, but I kind of like it that the graders are so reluctant to give a point. You have to respect them for that. When I saw how they grade, I felt a bit ashamed that I am so soft on my students in Potsdam. These guys are really hard-nosed. I guess I've gone soft after eight years in a soft-skills (no pun intended) oriented linguistics department. Computer science and math at Ohio State was about as strict, although the math guys at OSU were a bit more relaxed, but only a bit.
My grades so far are as below (percentages). This excludes the first assignments; they do not count for the final grade. In general, these assignments count for 20% of the final grade. You have to get minimum 65% overall in the final grade (after the exams in June 2012) to be allowed to continue on to the MSc.
Average score of all homework assignments: 84.87%
Final exam scores: unknown.
Mathematics: mean score 93.4%
Assignment-1: 100%
## Notes: I was pleasantly surprised to get this grade, but I do admit the problems were not too hard. The hardest part of this course is not the math but the probability theory.
Assignment-2: 97%
## Made a stupid mistake. Don't ask.
Assignment-3: 81%
## Here, I lost a lot of points for not generalizing my solution for a particular proof, and I made a stupid mistake in a partial derivative computation (forgot to treat y as a constant when differentiating with respect to x) that caused a snowball-effect error in the final answer, and I thought that level curves are three-dimensional and plotted them as such. All errors could have been avoided if I had carefully re-read what I'd done, but there was no time (this was also the only submission so far which was not typeset, perhaps another reason why I didn't notice the errors---when typesetting I usually discover a lot of mistakes in my solutions, esp. since I check my solutions at that stage with R or a computer algebra system like yacas).
Assignment-4: 100%
## Several people got 100% I believe. It was relatively easy because it was about really basic linear algebra mostly.
Assignment-5: 89%
## The first quartile was 83% it seems, and the third was 97%, so I clearly did not do well. I made some amazingly stupid arithmetic errors (like putting in a negative sign where there was supposed to be none), and it just adds up (or subtracts off). I had a hard time with one problem involving the computation of eigenvectors, and with a change of variables problem. I also made a stupid mistake in a double integral (miscopying one line onto the next, how dumb is that). All costly mistakes.
Probability: mean score 78.8%
Assignment-1: 76%
## Notes: I did relatively badly in the first assignment because I reversed a couple of signs accidentally, and because I didn't leave enough time for working on the assignment. I lost a lot of points on a stupid and mindless exercise involving reading numbers off of a binomial probability table --- shame on me.
Assignment-2: 96%
## Notes: The instructor cut 4 percentage points when I said that a particular distribution (I discovered later that this was the Cauchy distribution) had expectation infinity. He said I should have said "expectation does not exist." He's right, of course, but it was a painful loss, given that I didn't know at that time that infinity cannot be considered to exist in this particular context. That's a painful lesson.
Assignment-3: 70%
## Notes: I lost a lot of points for small things, like not defining a random variable X before I mention it (I thought it was clear from context, but I see that technically one has to define everything---God, I am out of touch with formal proofs and such like). The moral was that I have to write a lot more precisely. Perhaps there will be an improvement in the next submission's grades.
Assignment-4: 88%
## I made lots of small errors, and they add up.
Assignment-5: 64%
## Very hard assignment, done in a hurry because exams were imminent. Everyone's grades suffered. 64% was above average.
Statistics: mean score 82.4%
Assignment-1: 84%
Assignment-2: 82%
### It is amazing that the one thing I thought I could do---data analysis---is
## giving me the most trouble in this course. The grading is pretty harsh; for example, if you report a p=0.30 and don't say explicitly that you reject the null hypothesis, you lose points. I did make some horrible mistakes in this assignment though, so I do deserve losing some marks.
Assignment-3: 88%
## I got almost everything right, but I lost most of those 12% points for not defining \mu whenever I set up the null hypothesis. I was a bit crestfallen that most of those 12% points were cut for a repeated failure to define \mu (I felt it was clear from context what mu was in each case...).
Assignment-4: 84%
## I'm actually surprised I do so badly in the stats segment, compared to the other ones (math and probability).
Assignment-5: 74%
## Also done in a hurry. I don't know how the others did.
The textbooks:
One minor gripe I have in the course is some of the textbooks assigned. I think the course designers should probably invest some time into building complete course-specific lecture notes. Sometimes they do provide lectures notes, and these are great (my only complaint is that the authors don't believe in page numbers, which can be a real hassle if you print out the material and accidentally drop them on the floor). But that said, I realize that producing customized lecture notes is a major undertaking and I don't blame them for relying on existing books.
The math textbook is by Gilbert and Jordan, Guide$^2$ Mathematical Methods. The title is a bit strange, I mean the 2 instead of "to" (although the authors cannot be blamed for this naming decision---apparently Macmillan has a Guide 2... series). The book has one positive aspect: it covers the relevant material in the sense that it goes through the topics. So, for someone like me, who doesn't know exactly what I need to know as background to read more advanced textbooks on statistics, this is a good extended listing of the things I should know (or recall from high school). This is all good. What makes the reader's life hard are the super-terse proofs/solutions to exercises, and the large number of typos (especially in the solutions). The course organizers released a list of typos for the book at the start of the course, but there are even more typos than in the errata. The notation can also be sloppy and the reader has to be careful (e.g., at one point they write F-p, where F are the *names* of a function; what they meant was F(x)-p(x)).
An example of the terseness is the proof that the limit of sin(x)/x when x approaches 0 is 1. I had no idea where that proof was going until I watched Strang's online lecture (MIT open courseware). After watching Strang's lecture, I was able to unpack the proof myself, but I doubt that it could be done easily by just working through it (are proofs meant to be hard work to unpack? Read the Salas et al book on Calculus to see that the answer may be no). Gilbert and Jordan should read Knuth's book on writing mathematics. I would recommend Strang's lectures, and Calculus by Salas, Hille and Etgen (I have the 9th Edition); this last book really nailed it for me. This book has the smoothness and feel of Cormen, Rivest et al on Algorithms.
The probability theory book (Ross, A First Course in Probability) is OK in that it covers all the points. But it has the irritating property that each definition is followed by half a dozen totally unrelated examples. This in itself is not bad, but the examples are SCARY. I'm not sure I need to see the toughest applications of the latest idea learnt right away. After a bit of reading this sort of teaching-by-example at least this reader just gets depressed (there is no way I would have worked out those example answers myself after just reading the definitions provided immediately earlier). I found the online book by Jay Kerns much, much more useful for the present course---the course organizers should consider switching to that or at least assigning it alongside Ross, with some warnings to not get intimidated by Ross' style. Here is an excellent review of the Ross book on amazon that pretty much summarizes the main problems in the book.
There is an accompanying book on probability (by Freund, but authors are Miller and Miller) which is a straightforward and formal introduction to mathematical statistics; I like that more. It's part of the statistics course, not the probability course.
The statistics textbook is by Moore, McCabe and someone else, is absolutely terrible (apparently I'm not the only one complaining; see here). The book seems to be written for first year undergrads in statistics (nothing wrong with that of course, but this graduate certificate has a different audience). The large number of disconnected and silly examples (for example, for planned experiments vs observational studies) following every new concept lead to a feeling of total disorientation. There is also a painful attempt to make the book relevant to the modern user: examples about cell phones and iPhone Apps abound, presumably to draw in the young reader's eyes away from the cell phone as they read. The book could be a lot slimmer if all the extraneous junk is removed and they just stick to the facts presented.
There are so many really good books on introductory statistics using R (e.g., in the Use R! series); I wish they had used one of them. As it is, you have to be either real good at R, or be able to quickly get on board with R, if you want to do this course. Since the course is completely based on R, it is absolutely wonderful for me, but several of the students went into a state of blind panic (for example, a beginner often cannot easily figure out how to find out how to change a directory within R---in my own courses at Potsdam, I think we spend about 90 minutes just getting them used to the interface). Using an R-based book for introductory statistics would have been much better than Moore et al's. I have to admit though that I cannot name an alternative to Moore et al's right away that covers exactly the same material. I would like the book a lot more if there was a version for grown-up people: no photos of people holding cell phones, no extended and long-drawn out examples, just the facts.
I have concluded that the linear algebra books assigned in this course suck. They never tell you why one should care about such and such fact, and they overload the book with proofs. Also, linear algebraists apparently think they have a great sense of humor. Both Allenby and Lay, the former a bit more, deliver lots of intended-to-be-funny comments followed by an exclamation point. Lay can be very clear, though.
If anyone wants their first contact with linear algebra to be not painful, they should read Leonard Evens' excellent online book, which he has the generosity to release for free: http://www.math.northwestern.edu/~len/LinAlg/index.html. (I find it embarrassing that he wrote such a beautiful book and released it for free, whereas I have Springer charge for mine. Never again.) On the other hand, all these people writing expensive linear algebra texts should also be feeling a bit embarrassed to be out-performed by a free textbook (my super-expensive Lay textbook doesn't even have all the pages, some 10-20 pages are simply not there; the publishers apparently screwed up, and the table of contents page numbering bears no relationship to the actual numbers, so the table of contents is not only useless but actually misleading). Evens released his book with essentially no restrictions, with the source code. I really admire that.
I also found Gilbert Strang's book and online lectures on matrix algebra very cool. Denis Auroux's lectures are also quite amazing.
One thing worth noting about this course---I was not prepared for this---is that the last five lectures (out of 40) in each module (math, probability, and statistics) are the most demanding. I really had to sweat over this part of the course in a way I never had to for the earlier parts. Part of the reason is that these last five lectures deploy a lot of the material you learnt in the last 35 lectures, and obviously I don't have everything in my head and easily retrievable, so it was hard going to try to recall, for example, how to differentiate this or that function.
The concepts involving the method of moments, maximum likelihood estimates, likelihood ratio tests (in statistics); linear algebra, double integrals using polar coordinates and change of variables (math), and such like things were really overwhelming as they came in all at once towards the end. It doesn't help that the textbooks give pretty obscure discussions about this; in this part of the course I really had to google my way through these topics, by watching MIT Opencourseware lectures and reading dumbed down versions of these topics. What I missed the most in the textbooks was the why: why are we doing this, in the sense that where is this going? These online resources explain this mysterious aspect very well. Normally, it's almost anti-intellectual to ask a question like "why are we learning this?", but here, I really needed to know where I am going when I do an LRT or use the Neyman-Pearson Lemma, for example, or why a null space is called a null space (Evens answers that question). What's most remarkable though is the sheer range of resources available on the web to answer these questions. A lot of people spent a lot of their valuable time helping out poor suckers like me, who just don't get it. MIT Opencourseware is to be congratulated for releasing (for free) videos of so many important lectures on math and linear algebra.
Some other minor gripes about the course
1. In one of the pages of Ross' book (our assigned text), he writes "...if \sigma=\infty....". Now, in one of the probability theory assignments (Assignment 3) I lost four percentage points for saying that E[X]=\infty. I lost marks because I should have written, "the mean does not exist." This is correct, you do have to write exactly that. But when I pointed out that Ross makes the same mistake, I was told that that was a slight abuse of notation but it's fine. Seems like if a statistician writes something incorrectly, it's OK, but not if a student writes the same thing (maybe this makes sense, if you think about it). If I had seen Ross' statement before writing my assignment solution, would I still deserve to lose 4 percentage points? I found this double standard irritating. I have to admit that I am just whining about losing those four points (and these four points contribute almost nothing to the final grade, as homework assignments count for only 20 percent of the final grade), and so I'm perhaps just being a sore loser.
2. The statement of some of the probability theory problems in the homework assignments was very unclear. It's hard to write unambiguously, that's understandable; but I would have expected clearly worded problems. Even worse, the clarifications one got after asking for more detail led to so much confusion among us students (at one point the lecturer was contradicting an earlier statement) that in one case we just gave up and went with our interpretation, which seemed according to the messages from lecturer to be wrong (I will report later if our interpretation got full marks or not; it turns out my own interpretation was correct, I got full marks). I was not the only one facing this problem; there was a flurry of unhappiness about the question. This is true for occasional other assignments (I would say in maybe 2% of all cases there was some ambiguity, so it's definitely not a serious issue). For example, in one of the stats assignments we have a garden-path that fooled a student:
"Compare this with what happens if you first include the interaction with the residual..."
The author of this assignment intended a non-local attachment of the prepositional phrase "with the residual" to "compare", not to "interaction". The student wanted to know how to compute "the interaction with the residual". A more common class of error is scope ambiguities (usually fatal ones). Maybe mathematicians and statisticians need to study formal semantics and syntax!
3. Too often, the response to clarification questions can take up to a week or more; this is simply too long a period for a course moving as fast as this one. In some cases, I just had to go with what I understood. This isn't too serious; one often leaves a course with many questions unanswered, and after all this course is just a prep course for the real thing, the MSc. But it could be optimized by asking the lecturers to check the message board at least once a day or every other day.
Final exams
The final exams were designed with the following assumptions in mind: (a) you are not expected to finish them on time unless you could immediately solve every problem without thinking much about it, or thinking extremely fast, (b) you can compute on the calculator extremely fast, (c) you have everything on your fingertips (the exam is open book, but one does not really have time to look things up). I think I'll be lucky if I make the 65% "passing" grade (passing in the sense that one can proceed to the MSc).
One mistake I made was that I should have regularly reviewed every single topic incrementally as the course progressed, and I should have kept doing exercises on old topics (e.g., integration techniques), so that I would not forget details from a few months ago. Next time I will be a lot more systematic in doing revision. Mathematicians are not kidding when they say you have to practice every single day; it's no different from playing the violin.
Conclusion
Overall, a thumbs-up. This is a course every non-statistician who needs to work with data should take. Even in these few months I learnt a lot of interesting and even downright cool things (mostly in the math segment, but also in probability theory).
The big advantages of doing this kind of structured course are that:
- you have to solve problems on a daily basis in order to the get the assignments done on time, and someone carefully checks your work. If you try to read books on topics that are specifically relevant to you, like Gelman recommends, you are not going to get that quality of feedback (no, not even with a solutions manual).
- you can ask a statistician questions that come up as you read or work on real problems that affect your own life, and they will often take the time to answer them fully. This is virtually impossible if you just try to talk to a random statistician (generally, they either heap scorn on you, or give a rambling answer that doesn't really answer the question, because they just don't want to pay attention long enough to try to understand the problem---not that I blame them for that; why should they care what your problem is?).
Some of the material I consulted while doing this course (incomplete):
1. On writing math
2. Kerns' book on probability
3. Grinstead and Snell on probability
4. Salas et al Calculus
5. Spivak Calculus
6. MIT Open courseware (Strang, Auroux on calculus and linear algebra)
I consulted many other books, I will put a list online one of these days.
Software I used in this course:
1. R
2. Yacas (with Ryacas and without), to check my answers, arrived at analytically.
3. Mathematica to check my solve-for-theta type of solutions.
4. Matlab (I forgot why I used Matlab instead of Mathematica, but I did).
What next?
So, now I know almost everything they taught in this course. This is supposed to be (almost?) equivalent to an undergrad degree in statistics, but I doubt that, because one cannot learn in nine months what others have spent three years learning. But I do know enough to move on to more advanced texts. After some asking around (Sheffield instructors) and doing some research, I concluded that I need to read two books completely:
1. Salas et al on Calculus; Strang and Auroux's lectures on calculus.
2. Shayle Searle's "Matrix Algebra useful for Statistics" (the graduate certificate teaches you almost everything in this book, but it's a nice review nonetheless, and talks about some details not covered in the course)
3. James Gentle on Matrix Algebra. Gentle's book seems to be a classic, but it's hard going so be prepared to read slowly.
4. Strang's lectures on calculus and matrix algebra (Strang's book on Matrix Algebra is also a pleasure to read, you can feel his personality shine through his words).
This material will cover pretty much all the math I would need for a good understanding of statistical theory. This is an incomplete list, of course, and it's based on my own conclusions about what is needed, so it may not even be the right list.
Sunday, November 06, 2011
How to present one's reviewing service in one's cv
I've been listing my reviewing service as an enumerated list in my cv till now, but recently I saw a better option: Brian Roark's cv has a semi-graphical representation of his reviewing record. His presentation is ugly IMHO, but the idea is great. So, inspired by his example, I came up with this as a first attempt:
The code goes like this:
The data file has the outlet (journal etc. name) and year, sorted by the number of times I reviewed for that outlet.
> head(data)
outlet year count.sum
9 Brain_Research 2006 1
10 CBG 2010 1
11 CJAL 2012 1
28 DFG 2007 1
29 Dial_and_Discourse 2010 1
30 EACL 2012 1
Define the x and y axes:
And plot:
library(ggplot2)
The code goes like this:
The data file has the outlet (journal etc. name) and year, sorted by the number of times I reviewed for that outlet.
> head(data)
outlet year count.sum
9 Brain_Research 2006 1
10 CBG 2010 1
11 CJAL 2012 1
28 DFG 2007 1
29 Dial_and_Discourse 2010 1
30 EACL 2012 1
Define the x and y axes:
y<-data$year
x<-data$outlet
And plot:
library(ggplot2)
(p<-qplot(x,y,geom=c("point"),
alpha=I(2/3),ylab="year",xlab="journals/conferences/funding agencies/other",main=paste("summary of reviewing service (2003-2011); ",n," items \n public version [sorted by frequency] \n current as of ",Sys.Date()),position=position_jitter(w=0, h=.2))+coord_flip())
Suggestions for improvement are most welcome.
This presentation has so many advantages over a listing: it tells you whom I reviewed for most, and it's more compact.
Of course, I have two versions of this plot, one is public (the one above), and the other is private (because I review for universities and don't want to violate confidentiality). I have a switch in latex that generates a public or private version:
In the preamble write:
\ifx\UseOption\undefined
\def\UseOption{optb}
\fi
\usepackage{optional}
Then the public version goes like this:
%% public version
\opt{optb}{
\begin{figure}[htbp]
\begin{center}
\includegraphics[width=9cm]{"reviewingpublic"}
\caption{ACL: Association of Computational Linguistics; AMLaP: Architectures and Mechanisms for Language Processing; BRM: Behavior Research Methods;
CBG: Copenhagen Business School;
CUNY: CUNY Sentence Processing Conference; Cog\_Sci: Cognitive Science; Cog\_Sci\_Conf: Cognitive Science Conference; DFG: Deutsche Forschungsgemeinschaft; Dial\_and\_Discourse: Dialogue and Discourse; EACL: European ACL; ETAP: Experimental and Theoretical Approaches in Prosody; ESF: European Science Foundation; ICCM: International Conference on Cognitive Modeling; JML: Journal of Memory and Linguistics; J\_Jap\_Ling: Journal of Japanese Linguistics; J\_of\_Ling: Journal of Linguistics; LCP: Language and Cognitive Processes; Lang\_and\_Speech: Language and Speech; Ling\_Evidence: Linguistic Evidence; NLLT: Natural Language and Linguistic Theory; NSF: National Science Foundation (USA); NWO: Netherlands Organization for Scientific Research; PBR: Psychological Bulletin and Review; Research\_Lang\_Comp: Research on Language and Competition; TiCS: Topics in Cognitive Science.}
\label{reviewing}
\end{center}
\end{figure}
}
And the private version goes like this:
\opt{opta}{your figure here}
When compiling one does (> is the command line):
for the public version:
> pdflatex vasishthcv.tex
for the restricted version:
> pdflatex -jobname vasishthcv "\def\UseOption{opta}\input{vasishthcv}"
Monday, October 31, 2011
Graduate certificate in statistics
I finally have a sabbatical; such a relief not to have to teach for a bit. What can one usefully do during a sabbatical? Here's a preliminary list:
(a) bird watching
(b) lounge around
(c) check email relentlessly
(d) surf the web for six months straight
(e) do a statistics degree
I decided to go for (e). I never really learned statistics systematically (some would say, not at all, and they would not be far off the mark ;), which is absurd if you consider that it's practically my bread and butter (using statistics for data analysis). Why isn't everyone in psycholinguistics a professional statistician? God knows we all need that expertise.
So I surfed the web a bit and found something that kills two birds with one stone. A part time distance MSc in statistics, at Sheffield. Time commitment is 20 hours a week (i.e., 3 hours a day if you work on it seven days a week); very minimal I would say. If I cut out on reading fiction and other non-work books in the evenings after dinner, that's three hours right there every day.
At Ohio State, one of my professors, Brian Joseph, related the story of a physicist at OSU who decided to learn Sanskrit by taking one of Brian's classes; he did his studies in the evenings after dinner. Before long he was teaching the course with Brian. So my only question is: why the hell didn't I think of formally learning statistics earlier?
I'm doing the prep course first, to review the math, stats, and probability theory that is assumed for the MSc, and plan to start the MSc next year (I do have to pass the prep course, would be pretty annoying if I failed ;). And the course is great! I never realized back in school that math is FUN, probability theory is FUN, I only understood that once I got to Ohio State. And I'm again enjoying struggling with unfamiliar problems. The only annoying thing is that the homework assignments have to, of course, be submitted online, and so I feel compelled to typeset them nicely using Sweave+LaTeX, which is very time consuming. At Ohio State I never did that, I just wrote them up by hand (e.g., in formal language theory or discrete math or logic classes). Somehow the idea of an online submission demands typesetting, I can't bring myself to write it with a pn, scan the solution, and send it...
The course itself is good so far (too early to tell; e.g., in the stats segment we are drawing boxplots "by hand", which I did for the first time in my life today). But the textbooks could have been better, IMHO.
Thursday, September 01, 2011
Lower p-values apparently give you more confidence in the alternative hypothesis
"But an isolated finding, especially when embodied in a 2 X 2 design, at the .05 level or even the .01 level was frequently judged not sufficiently impressive to warrant archival publication." (p. 554)
From: Melton, A. W. (1962). Editorial. Journal of Experimental Psychology, 64, 553–557.
According to Gigerenzer et al (Published in: D. Kaplan (Ed.). (2004). The Sage handbook of quantitative methodology for the social sciences (pp. 391–408)), this quote is where the common convention comes from to use p-values as a measure of one's belief in a result.
Gigerenzer et al write:
"Editors of major journals such as A. W. Melton (1962) made null hypothesis testing a necessary
condition for the acceptance of papers and made small p-values the hallmark of excellent
experimentation."
Sunday, July 17, 2011
Potsdam Mind Research Repository
Here's a revolutionary website: all data and code accompanying papers.
http://read.psych.uni-potsdam.de/pmr2/
Imagine if it was mandatory to release data with your publication! It would make life so much easier.
http://read.psych.uni-potsdam.de/pmr2/
Imagine if it was mandatory to release data with your publication! It would make life so much easier.
Thursday, December 09, 2010
Friday, October 15, 2010
Wednesday, September 29, 2010
tilde's in URLs (LaTeX)
Obscure LaTeX command:
\textasciitilde{} % for tilde's in URLs as text.
I'd been using $\sim$.
\textasciitilde{} % for tilde's in URLs as text.
I'd been using $\sim$.
Saturday, September 25, 2010
Public and private cv's (LaTeX)
Not directly related to statistics but:
Often one wants to have a public cv that one can put on the web, and a more restricted one that has private information that one only needs for a job application or something. Instead of maintaining two cvs, there's an easy way to automate it if you are a latex user.
1. For a public cv, type:
## public
pdflatex vasishthcv.tex
2. For a restricted cv, type:
## restricted
pdflatex -jobname vasishthcv "\def\UseOption{opta}\input{vasishthcv}"
where in the tex file, you have in the preamble:
\ifx\UseOption\undefined
\def\UseOption{optb}
\fi
\usepackage{optional}
and
in the text itself for restricted sections use:
\opt{opta}{Home address:...}
Often one wants to have a public cv that one can put on the web, and a more restricted one that has private information that one only needs for a job application or something. Instead of maintaining two cvs, there's an easy way to automate it if you are a latex user.
1. For a public cv, type:
## public
pdflatex vasishthcv.tex
2. For a restricted cv, type:
## restricted
pdflatex -jobname vasishthcv "\def\UseOption{opta}\input{vasishthcv}"
where in the tex file, you have in the preamble:
\ifx\UseOption\undefined
\def\UseOption{optb}
\fi
\usepackage{optional}
and
in the text itself for restricted sections use:
\opt{opta}{Home address:...}
Friday, December 11, 2009
Statistics in linguistics
People in linguistics tend to treat statistical theory as something that can be outsourced--we don't really need to know anything about the details, we just need to know which button to click.
People easily outsource statistical knowledge in an empirical paper, but the same people would be appalled if they hired an assistant to work out the technical details of syntactic theory for a syntax paper.
The statistics *is* the science, it's not some extra appendage that can be outsourced.
People easily outsource statistical knowledge in an empirical paper, but the same people would be appalled if they hired an assistant to work out the technical details of syntactic theory for a syntax paper.
The statistics *is* the science, it's not some extra appendage that can be outsourced.
Thursday, April 23, 2009
How to get ESS style indentation in textmate
This should be standard in Textmate, I don't know why one has to go through so many steps to get it working:
http://gragusa.wordpress.com/2007/11/11/textmate-emacs-like-indentation-for-r-files/
http://gragusa.wordpress.com/2007/11/11/textmate-emacs-like-indentation-for-r-files/
How to update R bundle in textmate
Got this from the web somewhere:
Just create a script with the following content:
#!/bin/sh
LC_CTYPE=en_US.UTF-8
SVN=`which svn`
echo Changing to Bundles directory...
mkdir -p /Library/Application\ Support/TextMate/Bundles
cd /Library/Application\ Support/TextMate/Bundles
if [ -d /Library/Application\ Support/TextMate/Bundles/R.tmbundle ]; then
echo R bundle already exists - updating...
$SVN up "R.tmbundle"
else
echo Checking out R bundle...
$SVN --username anon --password anon co http://macromates.com/svn/Bundles/trunk/Bundles/R.tmbundle/
fi
echo Reloading bundles in TextMate...
osascript -e 'tell app "TextMate" to reload bundles'
Just create a script with the following content:
#!/bin/sh
LC_CTYPE=en_US.UTF-8
SVN=`which svn`
echo Changing to Bundles directory...
mkdir -p /Library/Application\ Support/TextMate/Bundles
cd /Library/Application\ Support/TextMate/Bundles
if [ -d /Library/Application\ Support/TextMate/Bundles/R.tmbundle ]; then
echo R bundle already exists - updating...
$SVN up "R.tmbundle"
else
echo Checking out R bundle...
$SVN --username anon --password anon co http://macromates.com/svn/Bundles/trunk/Bundles/R.tmbundle/
fi
echo Reloading bundles in TextMate...
osascript -e 'tell app "TextMate" to reload bundles'
Wednesday, July 04, 2007
Selection bias in journal articles
Journals dealing in psycholinguistic research do not publish null results generally, because they are "inconclusive". So it's completely possible that out of 100 experiments, 95 are inconclusive, and 5 are "significant", but that all five are Type I errors. But it's those 5 experiments that will get published.
The naive rebuttal to this would be that such a situation would only rarely arise. But the non-obvious thing is that rare events do happen. If we published only those five articles, then how would we draw the conclusion that we are not in Type I la la land?
The naive rebuttal to this would be that such a situation would only rarely arise. But the non-obvious thing is that rare events do happen. If we published only those five articles, then how would we draw the conclusion that we are not in Type I la la land?
Saturday, April 28, 2007
Rlang mailing list
Roger Levy has created a possibly useful wiki for exchanging questions about the use of R for language research:
https://ling.ucsd.edu/mailman/listinfo.cgi/r-lang
https://ling.ucsd.edu/mailman/listinfo.cgi/r-lang
Saturday, April 21, 2007
How to choose between a multiplicity of sexy models
It's websites like this that give model selection such a bad reputation in science:
http://www.modelselection.org/
http://www.modelselection.org/
A blog most amazing
I just found a most astounding blog via Gelman's blog:
http://emotion.inrialpes.fr/~dangauthier/blog/
http://emotion.inrialpes.fr/~dangauthier/blog/
Tuesday, April 17, 2007
How to extract SEs from lmer fixed effects estimates
Extracting fixed effects coefficients from lmer is easy:
fixef(lmer.fit)
But extracting SEs of those coefficients is, well, trivial, but you have to know what to do. It's not obvious:
Vcov <- vcov(lmer.fit, useScale = FALSE)
se <- sqrt(diag(Vcov))
fixef(lmer.fit)
But extracting SEs of those coefficients is, well, trivial, but you have to know what to do. It's not obvious:
Vcov <- vcov(lmer.fit, useScale = FALSE)
se <- sqrt(diag(Vcov))
Saturday, February 17, 2007
Hmisc: how to increase magnification
One non-obvious thing (at least to me) about Hmisc's xYplot function is that to increase magnification or other parameters of a graph component, you have to do the following.
xlab=list("Condition",cex=2)
I.e., you have to make a list out of the parameter, and add whatever information you need. This works generally for any of the xYplot parameters.
xlab=list("Condition",cex=2)
I.e., you have to make a list out of the parameter, and add whatever information you need. This works generally for any of the xYplot parameters.
Thursday, January 25, 2007
using winbugs with gelman and hill book on intel macs
I finally installed Windows on my Mac (a traumatic experience) and finally got the code working. However, the startup instructions on the website of the book did not work for me. I offer a working example for other souls as clueless as myself. The first problem is that the libraries have to be installed manually, they do not install automatically as adverstised. Second, the library R2WinBUGS has to be called explicitly to run the critical bugs command.
Also, if anyone out there is thinking of installing a dual boot environment in Mac in order to install WinBUGS, there is a bug (no pun intended) in the licence installation of WinBUGS. The decode command for the license does not work as advertised, but the license installs anyway.
The working version is here: http://www.ling.uni-potsdam.de/~vasishth/temp/schools2.R
Also, if anyone out there is thinking of installing a dual boot environment in Mac in order to install WinBUGS, there is a bug (no pun intended) in the licence installation of WinBUGS. The decode command for the license does not work as advertised, but the license installs anyway.
The working version is here: http://www.ling.uni-potsdam.de/~vasishth/temp/schools2.R
Monday, January 22, 2007
Some expensive lessons I recently learnt about R/Sweave
1. If you are going to generate lots of latex tables automatically from an Rnw file, LABEL THEM.
2. weaver does not work with xYplot. If you are using the Hmisc library, just don't use weaver. I will present a solution here sometime soon.
The solution: set caching to off (cache=off) in the chunk that loads the Hmisc library and runs the xYplot command(s). You can turn caching on before and after the chunk, but xYplots need to be computed without caching.
3. xtable is unable to identify the fact that an R output line containing, e.g., log(sigma^2), has to be in math-environment in the tex. In Sweave this has the disastrous consequence that the .tex file does not compile. My kludgy solution is to search and replace the .tex file after Sweaving it.
It's frustrating that such good tools can sometimes be such a pain in the ass. I guess one should be grateful they are there at all.
2. weaver does not work with xYplot. If you are using the Hmisc library, just don't use weaver. I will present a solution here sometime soon.
The solution: set caching to off (cache=off) in the chunk that loads the Hmisc library and runs the xYplot command(s). You can turn caching on before and after the chunk, but xYplots need to be computed without caching.
3. xtable is unable to identify the fact that an R output line containing, e.g., log(sigma^2), has to be in math-environment in the tex. In Sweave this has the disastrous consequence that the .tex file does not compile. My kludgy solution is to search and replace the .tex file after Sweaving it.
It's frustrating that such good tools can sometimes be such a pain in the ass. I guess one should be grateful they are there at all.
Saturday, January 13, 2007
Incomplete Review of Gelman and Hill's Data Analysis using Regression and Multilevel/Hierarchical Models
I'm writing this somewhat cranky review as I read the book. Compared to the Pinheiro and Bates book, the examples in this book are initially irritatingly difficult to get working. A major problem with the book is that code involving BUGS runs only on Windows. This excludes readers like me from the action. So I have to wait until I get a Windows machine--but do I really want to start using Windows now? It would have been more helpful if their webpage prominently mentioned this detail (that the book is Windows specific). Had they done that I would probably not have bought it. But now that I have paid for it I am going to read it.
The website for the book has the data in a pretty disorganized way--why not just make a library? The authors do have a package for arm on the CRAN archive, but it does not install on any OS except Windows (the first R package I have seen with this property in my seven years as an R user). I tried to wget -r the ~gelman/arm/examples directory but ended up with all kinds of other crap in my directory as well, which was annoying. A zip archive could not hurt.
Chapters 1-3
I did not get a huge amount out of these chapters that was deeply interesting, but it is a good intro for newcomers to regression.
The code for the example in chapter 3 doesn't work on non-windows machines. Here is a working version.
Chapter 4
The book becomes more and more exciting from about this point onwards. Only one grouse:
Chapter 4 has some principles doing carrying out regression for prediction (section 4.6) but it is far from clear where they come from and the principles have a cookbookey feel (do this, don't do that, without explaining why). It would have been better if the authors had taught the reader to reason about the problem (surely those are the real principles, and the presented principles the consequences of the thought process generated by those principles).
[to be continued]
The website for the book has the data in a pretty disorganized way--why not just make a library? The authors do have a package for arm on the CRAN archive, but it does not install on any OS except Windows (the first R package I have seen with this property in my seven years as an R user). I tried to wget -r the ~gelman/arm/examples directory but ended up with all kinds of other crap in my directory as well, which was annoying. A zip archive could not hurt.
Chapters 1-3
I did not get a huge amount out of these chapters that was deeply interesting, but it is a good intro for newcomers to regression.
The code for the example in chapter 3 doesn't work on non-windows machines. Here is a working version.
Chapter 4
The book becomes more and more exciting from about this point onwards. Only one grouse:
Chapter 4 has some principles doing carrying out regression for prediction (section 4.6) but it is far from clear where they come from and the principles have a cookbookey feel (do this, don't do that, without explaining why). It would have been better if the authors had taught the reader to reason about the problem (surely those are the real principles, and the presented principles the consequences of the thought process generated by those principles).
[to be continued]
Thursday, January 04, 2007
Wednesday, January 03, 2007
Null hypotheses, significance testing and all that jazz
Some amazing articles I've recently read in my ample spare time:
1. The Insignificance of Null Hypothesis Significance Testing
Jeff Gill
Political Research Quarterly, Vol. 52, No. 3 (Sep., 1999), pp. 647-674
doi:10.2307/449153
2. Andrew Gelman's article
3. And this one: http://www.npwrc.usgs.gov/resource/methods/statsig/index.htm
4. Bowers and Gelman on Exploratory Data Analysis with Hierarchical Linear Models (AKA Multilevel models)
Suitably stunned into silence, the reader may then have the following practical question: how to present one's HPD intervals in a journal, and what else to present?
Here's an answer from Doug Bates.
1. The Insignificance of Null Hypothesis Significance Testing
Jeff Gill
Political Research Quarterly, Vol. 52, No. 3 (Sep., 1999), pp. 647-674
doi:10.2307/449153
2. Andrew Gelman's article
3. And this one: http://www.npwrc.usgs.gov/resource/methods/statsig/index.htm
4. Bowers and Gelman on Exploratory Data Analysis with Hierarchical Linear Models (AKA Multilevel models)
Suitably stunned into silence, the reader may then have the following practical question: how to present one's HPD intervals in a journal, and what else to present?
Here's an answer from Doug Bates.
Tuesday, January 02, 2007
Great article: EDA for HLMs
There's an interesting paper I just read that comes with Sweave/R code that the article uses:
http://www-personal.umich.edu/~jwbowers/papers.html
It's called EDA for HLMs, and advocates an exploratory data analysis when trying to understand data (as opposed to blindly searching for a yes/no answer, did significance fall below 0.05). In psycholinguistics, we are still a long way from conventional plodding along well beaten paths.
http://www-personal.umich.edu/
It's called EDA for HLMs, and advocates an exploratory data analysis when trying to understand data (as opposed to blindly searching for a yes/no answer, did significance fall below 0.05). In psycholinguistics, we are still a long way from conventional plodding along well beaten paths.
Installing weaver
It is not immediately obvious how one can install weaver (thanks to balajis for telling me about it--see his comment to the Sweave speed issues).
Do the following as superuser for a system-wide install:
1. install digest (from CRAN)
2. install codetools from http://bioconductor.org/packages/1.9/omegahat/html/codetools.html
3. install weaver from http://www.bioconductor.org/packages/1.9/bioc/html/weaver.html
A clunky way to install on Mac OS X and Linux is: as superuser do
R CMD INSTALL packagetarball
I'll add information on how to use it later, but one can always consult the weaver manual/vignette.
Do the following as superuser for a system-wide install:
1. install digest (from CRAN)
2. install codetools from http://bioconductor.org/packages/1.9/omegahat/html/codetools.html
3. install weaver from http://www.bioconductor.org/packages/1.9/bioc/html/weaver.html
A clunky way to install on Mac OS X and Linux is: as superuser do
R CMD INSTALL packagetarball
I'll add information on how to use it later, but one can always consult the weaver manual/vignette.
How I maintain my data
As soon as you have a lot of experiments floating around, you tend to get a proliferation of code and data files. Usually, chaos ensues. If someone asks you for the data of some experiment you published, you can (a) ignore the request (this is the most economical but also the least ethical response) (b) send them they can realistically use. This post is about how to carry out (b).
Example.
Suppose I have a collection of data and R code that I will cryptically call intml.
1. package.skeleton("intml")
This will create some directories (see previous post)
2. now add the data to the data directory
3. add the .Rnw file you used to analyze the data as a vignette
Build a package as indicated in the last post, and send it to the person who asked for it. Or make it available on CRAN.
It's simple and it enforces a certain self-discipline. Nothing like the knowledge that anyone can read your code to force you to write it properly :-)
Example.
Suppose I have a collection of data and R code that I will cryptically call intml.
1. package.skeleton("intml")
This will create some directories (see previous post)
2. now add the data to the data directory
3. add the .Rnw file you used to analyze the data as a vignette
Build a package as indicated in the last post, and send it to the person who asked for it. Or make it available on CRAN.
It's simple and it enforces a certain self-discipline. Nothing like the knowledge that anyone can read your code to force you to write it properly :-)
Monday, January 01, 2007
Putting together a library
The Introduction to R and other documentation CRAN tells you how to build a library. But it is remarkably hard to find a step-by-step how-to for packaging together an R library. Here is a good one.
Subscribe to:
Comments (Atom)